চিরায়ত জ্যামিতিতে, কোন বৃত্ত বা গোলকের কেন্দ্র থেকে এর পরিধি পর্যন্ত অঙ্কিত যে কোন রেখাংশই ঐ বৃত্ত বা গোলকের ব্যাসার্ধ, আরো আধুনিক ব্যবহারের ক্ষেত্রে যাকে বৃত্ত বা গোলকের কেন্দ্র বলা হয়। একে বৃত্ত বা গোলকের পরিধির মধ্যকার দূরত্বও বলা হয়। গ্রীক dʌɪˈamɪtə (diameter) এর বাংলা পরিভাষা হিসেবে সংস্কৃত ব্যাস এবং ল্যাটিন ˈreɪdɪəs (radius) এর বাংলা পরিভাষা হিসেবে ব্যাসার্ধ শব্দটি নেওয়া হয়েছে। ল্যাটিন ভাষায় ˈreɪdɪəs শব্দের অর্থ রশ্মি, যষ্ঠি, অর, রথের চাকার স্পোক।[১] ব্যাসার্ধকে সংক্ষিপ্ত আকারে প্রকাশের ক্ষেত্রে সাধারণত r চলকটি ব্যবহার করা হয় এবং ব্যাস d কে ব্যাসার্ধের দ্বিগুণ হিসেবে সংজ্ঞায়িত করা:[২] d ≐ 2 r ⇒ r = d 2 .
যদি কোন বস্তুর কেন্দ্র না থাকে তবে একে পরিলিখিত বৃত্ত বা পরিলিখিত গোলকের ব্যাসার্ধ তথা পরিব্যাসার্ধ বলা যায়। উভয় ক্ষেত্রেই ব্যাসার্ধ কোন ব্যাসের অর্ধাংশকে বোঝানো ছাড়াও আরো বেশি কিছু নির্দেশ করতে পারে যেখানে সচরাচর একে একটি আকৃতির যেকোন দুটি বিন্দুর মধ্যকার সর্বোচ্চ দূরত্ব হিসেবে সংজ্ঞায়িত করা হয়। সাধারণভাবে কোন জ্যামিতিক আকৃতির মধ্যে আবদ্ধ বৃহত্তম বৃত্ত বা গোলকের ব্যাসার্ধই ঐ জ্যামিতিক কাঠামোটির অন্তঃব্যাসার্ধ। একটি বলয়, নল বা অন্য কোন ফাঁপা বস্তুর গহ্বরের ব্যাসার্ধ হল এর অভ্যন্তরীণ ব্যাসার্ধ।
কোন সুষম বহুভুজের ব্যাসার্ধ এর পরিব্যাসার্ধের মতই।[৩] একটি বহুভুজের কেন্দ্র থেকে এর যেকোন বাহুর মধ্যবিন্দু পর্যন্ত অঙ্কিত রেখাংশকে অ্যাপথেম বলা হয়। সুষম বহুভুজের অন্তঃব্যাসার্ধকেও অ্যাপথেম বলা হয়ে থাকে। গ্রাফ তত্ত্বে কোন লেখ বা গ্রাফের ব্যাসার্ধ হল u থেকে গ্রাফের যে কোন শীর্ষবিন্দুর সর্বোচ্চ দূরত্বের সকল u শীর্ষবিন্দুসমূহের মধ্যে সর্বনিম্ন দূরত্ব(?)।[৪]
C 
সূত্র
প্রায় সকল জ্যামিতিক কাঠামোর বিভিন্ন পরামিতির সাথে কাঠামোটির ব্যাসার্ধের একটি সুনির্দিষ্ট সম্পর্ক রয়েছে।
বৃত্ত
আরও দেখুন: বৃত্তের ক্ষেত্রফল
A 
P1, P2 ও P3 বিন্দু তিনটি সমরৈখিক বিন্দু না হলে এবং বৃত্তটি এদের উপর দিয়ে গমন করলে সাইনের সূত্র ব্যবহার করে ব্যাসার্ধকে নিম্নোক্তভাবে লেখা যায়— r = | O P 1 → − O P 3 → | 2 sin θ ,
এখানে θ হল ∠P1P2P3 কোণের মান। বিন্দু তিনটিকে (x1,y1), (x2,y2) এবং (x3,y3) কার্তেসীয় স্থানাংকে সূচিত করা হলে ব্যাসার্ধকে নিম্নরূপে প্রকাশ কার যায়— r = [ ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ] [ ( x 2 − x 3 ) 2 + ( y 2 − y 3 ) 2 ] [ ( x 3 − x 1 ) 2 + ( y 3 − y 1 ) 2 ] 2 | x 1 y 2 + x 2 y 3 + x 3 y 1 − x 1 y 3 − x 2 y 1 − x 3 y 2 | .
![{\displaystyle r={\frac {\sqrt {[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}][(x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2}][(x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2}]}}{2|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}|}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caffb954e8c39a26dcc5e4ad4f66494edd313008)
সুষম বহুভুজ
আরও দেখুন: পরিলিখিত বৃত্ত
| n | Rn |
|---|---|
| 3 | 0.577350… |
| 4 | 0.707106… |
| 5 | 0.850650… |
| 6 | 1.0 |
| 7 | 1.152382… |
| 8 | 1.306562… |
| 9 | 1.461902… |
| 10 | 1.618033… |
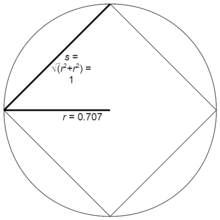
n=4 সংখ্যক বাহু যুক্ত সুষম বহুভুজ (বর্গ)
কোন সুষম বহুভুজের বাহুর সংখ্যা n এবং প্রতিটি বাহুর দৈর্ঘ্য s হলে এর ব্যাসার্ধ হবে— r = Rns
যেখানে, R n = 1 / ( 2 sin π n ) 
পরাঘনক
সাধারণভাবে চার বা ততোধিক মাত্রার যে জ্যামিতিক কাঠামোকে ত্রিমাত্রিক ঘনকের সমতূল্য বিবেচনা করা যায় তাকে পরাঘনক (hypercube) বলা হয়। s বাহু যুক্ত এবং d-মাত্রিক পরাঘনকের ব্যাসার্ধ হল— r = s 2 d .
স্থানাঙ্ক ব্যবস্থায় ব্যাসার্ধের ব্যবহার
কার্তেসীয়, মেরু, গোলীয়, বেলনাকার সহ অন্যান্য স্থানাঙ্ক ব্যবস্থায় ব্যাসার্ধের আবশ্যিক প্রয়োগ রয়েছে।
কার্তেসীয় স্থানাঙ্ক
মেরু স্থানাঙ্ক
মূল নিবন্ধ: পোলার স্থানাংক ব্যবস্থা
মেরু স্থানাঙ্ক ব্যবস্থা এক ধরনের দ্বি–মাত্রিক স্থানাঙ্ক ব্যবস্থা যেখানে কোন সমতলের প্রতিটি বিন্দুকে একটি নির্দিষ্ট বিন্দু থেকে এর দূরত্ব এবং একটি দিক নির্দিষ্ট থেকে কোণের মাধ্যমে সংজ্ঞায়িত করা হয়।
কার্তেসীয় ব্যবস্থার উৎসের সাথে তুলনীয় নির্দিষ্ট বিন্দুকে মেরু বলা হয় এবং মেরু থেকে নির্দিষ্ট দিকে অঙ্কিত রশ্মিকে মেরু অক্ষ বলে। মেরু থেকে অঙ্কিত দূরত্ব হল অরীয় বা রেডিয়াল স্থানাঙ্ক বা ব্যাসার্ধ এবং কোণটি হল কৌণিক স্থানাঙ্ক, মেরু কোণ বা দিগংশ।[৫]
বেলনাকার স্থানাঙ্ক
মূল নিবন্ধ: বেলনাকার স্থানাঙ্ক
বেলনাকার স্থানাঙ্ক ব্যবস্থায় একটি পছন্দ মাফিক (পূর্ব নির্ধারিত) প্রসঙ্গ অক্ষ এবং এই অক্ষটির লম্বদিকে একটি পছন্দ মাফিক (পূর্ব নির্ধারিত) প্রসঙ্গ তল থাকে। বেলনাকার স্থানাঙ্ক ব্যবস্থার উৎস এমন একটি বিন্দু যেখানে সকল তিন স্থানাঙ্ককে শূন্য ধরা যেতে পারে। এই ব্যবস্থা হল প্রসঙ্গ তল এবং অক্ষের অন্তচ্ছেদ।