BCS Question | Online Preparation

নির্ণায়ক

Written by

admin

in

নির্ণায়ক (ইংরেজি: Determinant) হলো বীজগণিতের একটি ফাংশন যা স্কেলার রাশি n-এর উপর নির্ভরশীল। একটি নির্দিষ্ট ধনাত্মক সংখ্যা n এর জন্য n×n ম্যাট্রিক্সের একটি অনন্য নির্ণায়ক ফাংশন আছে।

উল্লম্ব বার

ম্যাট্রিক্স A এর নির্ণায়ককে |A| দ্বারা প্রকাশ করা যায়। এই প্রকাশ পদ্ধতিটি কিছুটা দ্ব্যর্থবোধক, কেননা এটি ম্যাট্রিিক্সেের কিছু নর্ম এবং পরম মান প্রকাশের জন্যও ব্যবহার হয়ে থাকে। ম্যাট্রিক্স নর্মকে দুটি উল্লম্ব বার (e.g., ‖A‖) হিসেবেও উল্লেখ করা হয়ে থাকে, ফলে নির্ণায়ক প্রকাশে প্রথম পদ্ধতিটি প্রায়শই ব্যবহার হয়ে থাকে। উদাহরণস্বরূপ, ম্যাট্রিক্সের জন্য A = [ a b c d e f g h i ] A = \begin{bmatrix} a & b & c\\d & e & f\\g & h & i \end{bmatrix}\,

নির্ণায়ক det ( A ) \det(A) কে প্রকাশ করা হয় | A | |A| বা আরো নির্দিষ্টভাবে | A | = | a b c d e f g h i | . |A| = \begin{vmatrix} a & b & c\\d & e & f\\g & h & i \end{vmatrix}.\,

অর্থাৎ, বর্গাকৃতির বন্ধনীসমূহ দীর্ঘ উল্লম্ব বার দিয়ে প্রতিস্থাপিত হয়।

২x২ ম্যাট্রিক্সের নির্ণায়ক

সামান্তরিকের ক্ষেত্রফলটি হল এর বাহু নির্দেশক ভেক্টরগুলো থেকে সৃষ্ট মেট্রিক্সের নির্ণায়ক

2×2 ম্যাট্রিক্স হলো A = [ a b c d ] A = \begin{bmatrix} a & b\\c & d \end{bmatrix}\,

ম্যাট্রিক্সটির নির্ণায়ক হলো det ( A ) = a d − b c . \det(A)=ad-bc.\,

৩x৩ ম্যাট্রিক্সের নির্ণায়কসমূহ

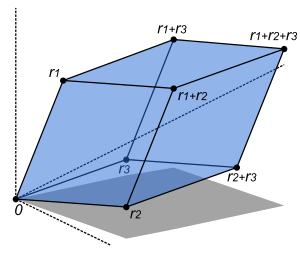
এই প্যারালালপিপেডটির আয়তন হল r1, r2, ও r3 সারির মেট্রিক্সের নির্ণায়কটির পূর্ণমান

The 3×3 matrix: A = [ a b c d e f g h i ] . A=\begin{bmatrix}a&b&c\\ d&e&f\\g&h&i\end{bmatrix}.

ম্যাট্রিক্সটির প্রথম সারিতে cofactor expansion ব্যবহার করে আমরা পাই: det ( A ) = a | e f h i | − b | d f g i | + c | d e g h | = a e i − a f h − b d i + c d h + b f g − c e g = ( a e i + b f g + c d h ) − ( g e c + h f a + i d b ) , \begin{align} \det(A) &= a\begin{vmatrix}e&f\\h&i\end{vmatrix} -b\begin{vmatrix}d&f\\g&i\end{vmatrix} +c\begin{vmatrix}d&e\\g&h\end{vmatrix} \\ &= aei-afh-bdi+cdh+bfg-ceg \\ &= (aei+bfg+cdh)-(gec+hfa+idb), \end{align}

৩x৩ মেট্রিক্সের নির্ণায়ক কোনাকুনি রেখা দিয়ে হিসাব করা যাবে

একে সহজভাবে মনে রাখা যাবে এভাবে, এটি হলো উত্তর-পশ্চিম থেকে দক্ষিণ-পূর্ব বরাবর তিনটি কোণাকুণি রেখার উপাদানগুলোর গুণফলের সমষ্টি থেকে দক্ষিণ-পশ্চিম থেকে উত্তর-পূর্বে তিনটি রেখার উপাদানের সমষ্টির বিয়োগফলের সমান যখন ম্যাট্রিক্সের প্রথম দুটি কলামের কপি নিম্নোক্ত উপায়ে লেখা হয় a b c a b d e f d e g h i g h − a b c a b d e f d e g h i g h \begin{matrix} \color{blue}a & \color{blue}b & \color{blue}c & a & b \\ d & \color{blue}e & \color{blue}f & \color{blue}d & e \\ g & h & \color{blue}i & \color{blue}g & \color{blue}h \end{matrix} \quad - \quad \begin{matrix} a & b & \color{red}c & \color{red}a & \color{red}b \\ d & \color{red}e & \color{red}f & \color{red}d & e \\ \color{red}g & \color{red}h & \color{red}i & g & h \end{matrix}

উল্লেখ্য যে, এই মনে রাখার রাখার পদ্ধতিটি উচ্চতর মাত্রার ক্ষেত্রে প্রযোজ্য নয়।

উদাহরণ

ধরা যাক, আমরা নিম্নোক্ত ক্ষেত্রে নির্ণায়কের মান নির্ণয় করতে চাই A = [ − 2 2 − 3 − 1 1 3 2 0 − 1 ] . A = \begin{bmatrix}-2&2&-3\\ -1& 1& 3\\ 2 &0 &-1\end{bmatrix}.

সরাসরি লাইবনিৎসের সূত্র ব্যবহার করে পাওয়া যাবে:

det ( A ) \det(A)\,= =\,( − 2 ⋅ 1 ⋅ − 1 ) + ( − 3 ⋅ − 1 ⋅ 0 ) + ( 2 ⋅ 3 ⋅ 2 ) (-2\cdot 1 \cdot -1) + (-3\cdot -1 \cdot 0) + (2\cdot 3\cdot 2)
− ( − 3 ⋅ 1 ⋅ 2 ) − ( − 2 ⋅ 3 ⋅ 0 ) − ( 2 ⋅ − 1 ⋅ − 1 ) - (-3\cdot 1 \cdot 2) - (-2\cdot 3 \cdot 0) - (2\cdot -1 \cdot -1)
= =\,2 + 0 + 12 − ( − 6 ) − 0 − 2 = 18. 2 + 0 + 12 - (-6) - 0 - 2 = 18.\,

এছাড়াও আমরা লাপ্লাস বিস্তার ব্যবহার করে নির্ণায়ককে কলাম ও সারির মাধ্যমে বর্ধিত করতে পারি। শূন্য আছে এমন একটি সারি বা কলাম ব্যবহার করা ভালো, তাই দ্বিতীয় কলামটি নিয়ে পাই:

det ( A ) \det(A)\,= =\,( − 1 ) 1 + 2 ⋅ 2 ⋅ det [ − 1 3 2 − 1 ] + ( − 1 ) 2 + 2 ⋅ 1 ⋅ det [ − 2 − 3 2 − 1 ] (-1)^{1+2}\cdot 2 \cdot \det \begin{bmatrix}-1&3\\ 2 &-1\end{bmatrix} + (-1)^{2+2}\cdot 1 \cdot \det \begin{bmatrix}-2&-3\\ 2&-1\end{bmatrix}
= =\,( − 2 ) ⋅ ( ( − 1 ) ⋅ ( − 1 ) − 2 ⋅ 3 ) + 1 ⋅ ( ( − 2 ) ⋅ ( − 1 ) − 2 ⋅ ( − 3 ) ) (-2)\cdot((-1)\cdot(-1)-2\cdot3)+1\cdot((-2)\cdot(-1)-2\cdot(-3))
= =\,( − 2 ) ( − 5 ) + 8 = 18. (-2)(-5)+8 = 18.\,
দেসগণিত

বিষয়শ্রেণীসমূহ:

More posts