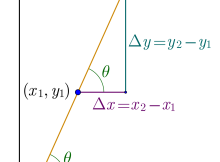ঢাল

ঢাল বা নতিমাত্রা হচ্ছে এমন একটি রেখা বা গ্রেডিয়েন্ট যা বর্ণনা করে এর দিক এবং কৌণিক মান।^[১]

ঢাল সাধারণতঃ ‌ m অক্ষর দ্বারা চিহ্নিত করা হয়।^[২]

একটি রেখার (যেকোনো) দুটি স্বতন্ত্র বিন্দুর মধ্যে “উল্লম্ব পরিবর্তন” থেকে “অনুভূমিক পরিবর্তন” এর অনুপাত খুঁজে বের করে ঢাল গণনা করা হয়। কখনও কখনও অনুপাতটি ভাগফল হিসাবে প্রকাশ করা হয়, একই রেখায় প্রতি দুটি স্বতন্ত্র বিন্দুর জন্য একই সংখ্যা দেয়। একটি রেখা যা কমছে তার একটি ঋণাত্মক “বৃদ্ধি” আছে।

বিশ্লেষণ

স্থানাঙ্ক জ্যামিতি ও ত্রিকোণমিতির সাহায্যে

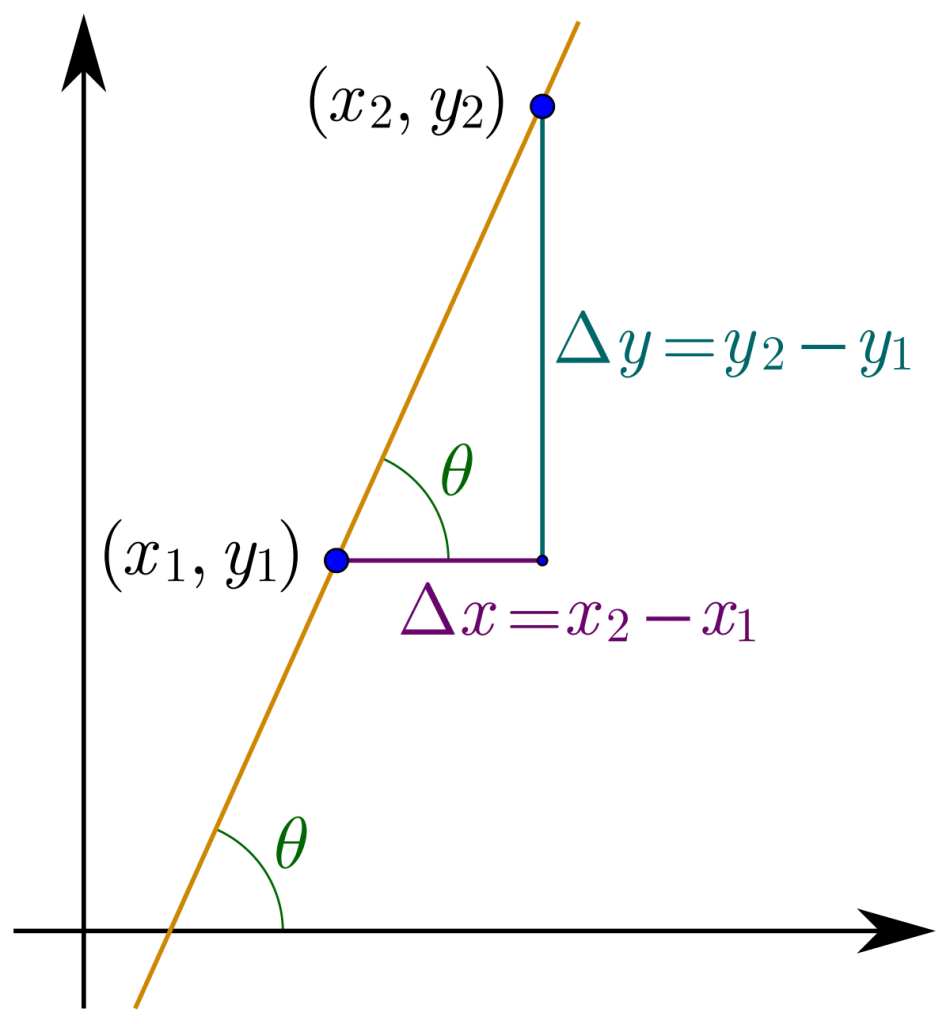
ধরি, ছক কাগজে দুটি বিন্দু ( x 1 , y 1 ) ও ( x 2 , y 2 ) । তাহলে বিন্দু দুটির সংযোজক সরলরেখার নতি হবে:- m = Δ y Δ x = y 2 − y 1 x 2 − x 1

আবার সরলরেখাটি x -অক্ষের সঙ্গে θ কোণে আনত থাকলে, সেক্ষেত্রে নতি হবে m = t a n θ

উপরের ছবিতে দেখা যাচ্ছে যে, একটি সমকোণী ত্রিভুজ তৈরী হয়েছে। সেখান থেকে,

m = t a n θ = y 2 − y 1 x 2 − x 1 = Δ y Δ x

অবকলনের সাহায্যে

নতিকে এভাবেও প্রকাশ করা যায়:

m = d y d x

কোন বক্ররেখার কোন বিন্দুতে নতি নির্ণয় করতে হলে, ওই বিন্দুতে স্পর্শক অঙ্কন করা হয়। তারপর নতি নির্ণয় করা হয়।

সরলরেখায় প্রয়োগ

y = m x + c সমীকরণটি সরলরেখার অন্যতম প্রধান সমীকরণ। এতে ব্যবহৃত m পদটি নতি নির্দেশ করে।

৪৫° রেখা

কোনো সরলরেখা মূলবিন্দুগামী হলে, যদি তার নতি ১ এর সমান হয়, তাকে ৪৫° রেখা বলে।

এটি y = m x + c সমীকরণটি মেনে চলে। এক্ষেত্রে c = 0 (যেহেতু y -অক্ষকে ( 0 , 0 ) বিন্দুতে ছেদ করে।)

মূলবিন্দুগামী যে কোনও সরলেখার সমীকরণ তাই y = m x ।

৪৫° রেখায় m = 1 হবার জন্য, এটির সমীকরণ হয়:- y = x

এখানে আবার নতিকোণ ( θ )=৪৫° বা π 4 হবার জন্যই, m = t a n π 4 = 1

সাধারণ সমীকরণে

সরলরেখার সাধারণ সমীকরণ:- a x + b y + c = 0 এখান থেকে নতি পাওয়া যায়, m = − a b

আরও দেখুন

• রেখা
• স্থানাঙ্ক জ্যামিতি
• অবকলন