সনাতন গণিতশাস্ত্রে স্থানাঙ্ক জ্যামিতি একটি গুরুত্বপূর্ণ শাখা। অনেক সময় একে বিশ্লেষণাত্মক জ্যামিতিও বলা হয়। এটি সাধারণত কো-অর্ডিনেট জ্যামিতি বা কার্টেসিয়ান জ্যামিতি নামে পরিচিত। এটি সিন্থেটিক জ্যামিতির সম্পূর্ণ বিপরীত।
পদার্থবিদ্যা ও কারিগরী শিক্ষায় এর গুরুত্ব অসীম।

চারটি বিভিন্ন বিন্দুকে স্থানাঙ্ক জ্যামিতির সহায়তায় উপস্থাপন। স্থানাঙ্ক হিসাবে (2,3) সবুজ, (−3,1) রঙা (−1.5,−2.5) নীল এবং মূল বিন্দু (0,0) বেগুনী
স্থানাঙ্ক জ্যামিতি হল জ্যামিতির একটি শাখা, যেখানে সমতলে অবস্থান করা একটি বিন্দুর স্থানকে এক জোড়া সংখ্যার সহায়তায় উপস্থাপন করা হয়। এই সংখ্যাজোড়কে স্থানাঙ্ক বলা হয়।[১] সমতলে একটি বিন্দুর অবস্থান জানতে একজোড়া অক্ষ ব্যবহার করা হয়। y-অক্ষ থেকে একটি বিন্দুর দূরত্বকে x-স্থানাঙ্ক বা ভুজ বলা হয়। x-অক্ষ থেকে একটি বিন্দুর দূরত্বকে y-স্থানাঙ্ক বা কোটি বলা হয়। x-অক্ষের উপরে থাকা একটি বিন্দুর স্থানাঙ্কের অবস্থান (x, 0) এবং y-অক্ষের উপরে থাকা একটি বিন্দুর স্থানাঙ্কের অবস্থান (0, y)।
স্থানাঙ্ক জ্যামিতির উপাদান সমূহের ধারণা
স্থানাঙ্ক জ্যামিতির ক্ষেত্রটিতে সাধারণত ব্যবহার হয়ে থাকা উপাদান সমূহের মধ্যে,
- x-অক্ষ এবং y-অক্ষ পরস্পরকে ছেদ করা বিন্দুর স্থানাঙ্ক (0, 0)
- x-অক্ষের ডান-পক্ষের মান ধনাত্মকএবং x-অক্ষের বাম-পক্ষের মান ঋণাত্মক।
- একইভাবে y-অক্ষের উপরের দিকে ধনাত্মক মান পাওয়া যায় এবং y-অক্ষের নিচে ঋণাত্মক মান সমূহ আসে।
- x-অক্ষ এবং y-অক্ষ পরস্পরকে ছেদ করে মোট চারটি চোখ সৃষ্টি করে এই চোখ সমূহের বিন্দু সমূহের মান (+, +), (-, +), (-, -), (+, -)হয়।
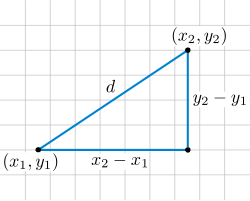
বিন্দুর মাঝের দূরত্ব উপস্থাপন
পরিসর
স্থানাঙ্ক জ্যামিতির পরিসর যথেষ্ট প্রভাবশালী। বীজগণিত, পদার্থবিজ্ঞান, মহাকাশ বিজ্ঞান, অভিযান্ত্রিক, নৌ বিদ্যা, ভূকম্প বিজ্ঞান কাল ইত্যাদি ক্ষেত্র সমূহে স্থানাঙ্ক জ্যামিতির বহুল প্রয়োগ করা হয়। যদি আমরা একজোড়া বিন্দুর স্থানাঙ্ক জানি তবে স্থানাঙ্ক জ্যামিতিকে আমরা বিভিন্ন দিকে ব্যবহার করতে পারি।
- বিন্দু সমূহের মধ্যে দূরত্ব নির্ণয় করতে পারা যায়।
সমতলে থাকা দুটি বিন্দু ( x 1 , y 1 ) 

আর এটি হল পিথাগোরাসের সূত্র। স্থানাঙ্ক জ্যামিতিতে একে ‘দূরত্ব সূত্র’ বলা হয়। এর দ্বারা একটি রেখার ভূমির সঙ্গে উৎপন্ন করা কোণের মানও নির্ণয় করা হয়। মূলবিন্দু ( 0 , 0 ) 

- কোনো রেখা খণ্ডের জন্য সমীকরণ, মধ্যমান, ঢাল ইত্যাদি নির্ণয় করা যায়।
- কোনো একটি রেখা উলম্ব না সমান্তরাল নির্ণয় করা যায়।
- সমতলে বিন্দু সমূহ সৃষ্টি করা বহুভুজ সমূহের পরিসীমা এবং ক্ষেত্রফল নির্ণয় করতে পারা যায়।
- কোনো একটি আকৃতিকে প্রতিবিম্বিত করতে স্থানান্তরিত তথা আবর্তন করতে এবং রূপান্তর করতে ব্যবহার করা যায়।
- উপবৃত্ত, বক্র, এবং বৃত্তর সমীকরণ নির্ণয় করতে।[২]
ইতিহাস
ভারতবর্ষ, গ্রিস, পারস্য ও ইউরোপের বিভিন্ন দেশে একক ভাবে এর উদ্ভব হয়েছিল।
গ্রীকগণিতবিদ মেনেসমাস কিছু গাণিতিক সমস্যা সমাধান এবং তত্ত্বসমূহ প্রমাণের জন্য একটি বিশেষ পদ্ধতি ব্যবহার করেছিলেন যেটি স্থানাঙ্ক জ্যামিতির সঙ্গে বিশেষভাবে সম্পর্কিত। কখনও কখনও তাঁকে অনেকে বিশ্লেষণাত্মক জ্যামিতি বা স্থানাঙ্ক জ্যামিতির প্রবর্তন করেছিলেন বলে বিশ্বাস করে।[৩] সমতলে বিন্দুর অবস্থান বর্ণনা করার পদ্ধতিটি ফরাসি গণিতবিদ রেনা ডেকার্টস্ (১৫৯৬ – ১৬৫০) এবং পিয়ের দ্য ফের্মা দ্বারা প্রস্তাবিত হয়েছিল।[৪][৫] তা হলেও রেনা ডেকার্টসের বহু সময়ে নাম নেওয়া হয়। [৬][৭] ডেকার্টসের নাম অনুসারে সেই স্থানাঙ্ক জ্যামিতিকে কার্টেসিয়ান জ্যামিতি বলা হয়। ১১শতকে পারস্য গণিতজ্ঞ ওমর খেয়াম জ্যামিতি এবং বীজগণিতের মধ্যে এক দৃঢ় সম্পর্ক উপস্থাপন করেছিলেন। তিনি জ্যামিতিক সমাধান দ্বারা সাধারণ বর্গীয় সমীকরণ নির্ণয়ের সাংখ্যিক এবং জ্যামিতিক বীজগণিতের মধ্যে থাকা দূরত্ব বের করেছিলেন।[৮][৯] অবশ্য ডেকার্টস দ্বারাই প্রকৃত একটি সিদ্ধান্তে উপনীত হওয়া হয়।[৮]


 .
. , যেখানে α
, যেখানে α  হচ্ছে ব্যাসার্ধ
হচ্ছে ব্যাসার্ধ , যেখানে C
, যেখানে C  একটি ধ্রুবক।
একটি ধ্রুবক। , যেখানে C
, যেখানে C  , যেখানে C
, যেখানে C 
 , বৃত্তচাপের বা সংশ্লিষ্ট বৃত্তের ব্যাসার্ধ r
, বৃত্তচাপের বা সংশ্লিষ্ট বৃত্তের ব্যাসার্ধ r  এবং বৃত্তচাপের প্রান্তবিন্দু দুটিকে সংযোগকারী
এবং বৃত্তচাপের প্রান্তবিন্দু দুটিকে সংযোগকারী ।
। একটি সমকোণী ত্রিভুজের
একটি সমকোণী ত্রিভুজের 
 ℓ = 2 r s − s 2 ,
ℓ = 2 r s − s 2 ,  or r = s 2 + ℓ 2 2 s = s 2 + ℓ 2 2 s .
or r = s 2 + ℓ 2 2 s = s 2 + ℓ 2 2 s . 

 .
. এর আসন্ন মান নির্ণয়ে নিম্নোক্ত সূত্র প্রয়োগ করা যেতে পারে— a ≈ ℓ + s 2 r
এর আসন্ন মান নির্ণয়ে নিম্নোক্ত সূত্র প্রয়োগ করা যেতে পারে— a ≈ ℓ + s 2 r 
 যেখানে a, b, এবং c হল ত্রিভুজের বাহুত্রয়ের দৈর্ঘ্য এবং D হল
যেখানে a, b, এবং c হল ত্রিভুজের বাহুত্রয়ের দৈর্ঘ্য এবং D হল 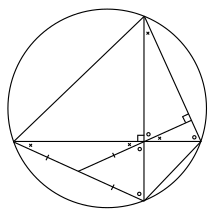


 এর মাধ্যমে। এখানে r হল ব্যাসার্ধ ভেক্টর। [[কার্তেসীয় স্থানাংক ব্যবস্থা|কার্তেসী স্থানাংক ব্যবস্থায় বিন্দুর অবস্থান প্রকাশ করা হয় (x,y) এর মাধ্যমে। কার্তেসীয় মাধ্যমে ব্যাসার্ধ ভেক্টর- r = ( x 2 + y 2 )
এর মাধ্যমে। এখানে r হল ব্যাসার্ধ ভেক্টর। [[কার্তেসীয় স্থানাংক ব্যবস্থা|কার্তেসী স্থানাংক ব্যবস্থায় বিন্দুর অবস্থান প্রকাশ করা হয় (x,y) এর মাধ্যমে। কার্তেসীয় মাধ্যমে ব্যাসার্ধ ভেক্টর- r = ( x 2 + y 2 ) 







![{\displaystyle r={\frac {\sqrt {[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}][(x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2}][(x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2}]}}{2|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}|}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caffb954e8c39a26dcc5e4ad4f66494edd313008)
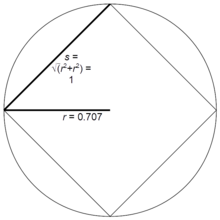
 । তালিকায় n এর ক্ষুদ্র মানের জন্য Rn মান দেওয়া হয়েছে। এছাড়াও এই মানগুলো s = 1 এর জন্য সংশ্লিষ্ট সুষম বহুভুজগুলির ব্যাসার্ধসমূকে নির্দেশ করে।
। তালিকায় n এর ক্ষুদ্র মানের জন্য Rn মান দেওয়া হয়েছে। এছাড়াও এই মানগুলো s = 1 এর জন্য সংশ্লিষ্ট সুষম বহুভুজগুলির ব্যাসার্ধসমূকে নির্দেশ করে।